【電気工事士１種過去問】抵抗が直列・並列接続した直流回路(R2年度問2)

問題＜R2年問2＞
図のような直流回路において、a-b間の電圧[V] は?

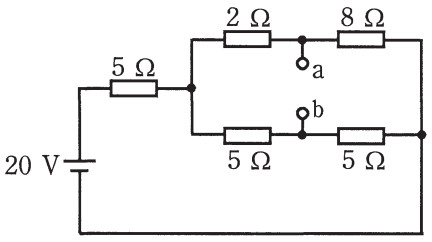
＜解答の選択肢＞
(計算問題のため、選択肢は省略)

— 答え —
a-b間の電圧は 3V。

【出典：令和2年度第一種電気工事士筆記試験問2】

解法と解説

抵抗だけの直流回路はサービス問題。必ず正解しよう。

動画のほうが分かりやすい方はこちらから。

複数の抵抗が接続された直流回路の解く手順は次の通り。

まず最初。赤枠で囲った直列接続の抵抗を合成すると、それぞれ 10Ωになる。

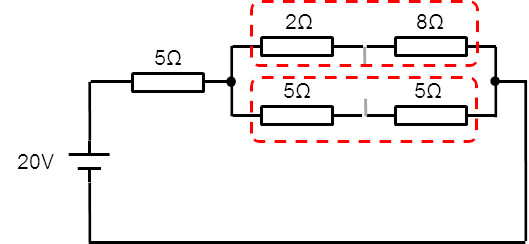
(合成後)

合成した2つの10Ω抵抗は並列接続だから、ここも合成する。すると、5Ω。

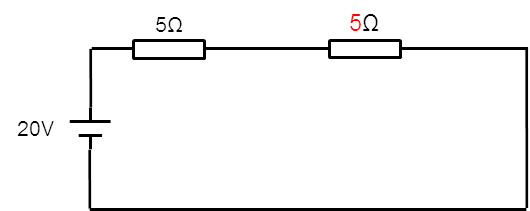
したがって、この回路は20V電源に 5Ωの抵抗が2個直列に接続されている。ここまでくれば、回路全体に流れる電流を求めることができる。

万全を期してもう1段階合成したいという人は、合成して「20V電源＋10Ω抵抗の回路」にする。

そうすると、回路全体に流れる電流 I_all は、
I_all = 20[V] / 10[Ω] = 2[A]
と分かる。

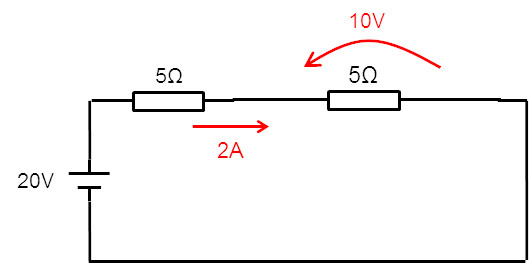
そしたら、右側の5Ω抵抗の両端の電圧は
V = I × R = 2 × 5 = 10[V]
と求まる。

今度は合成した抵抗を1つずつ戻していって、電流・電圧を求めていく。

まず、右側の5Ω抵抗は 10Ω抵抗の並列接続だったから、下図のように戻す。

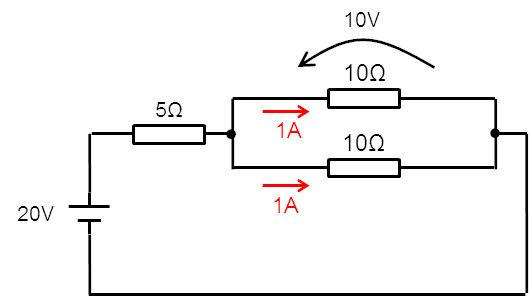
そして、抵抗両端の電圧は10Vだから、それぞれの10Ω抵抗のある回路(電線)には1Aずつ電流が流れる。

さらに10Ω抵抗を直列接続に戻すと、上側回路は “2+8Ω抵抗”、下側は “5+5Ω抵抗”だった。

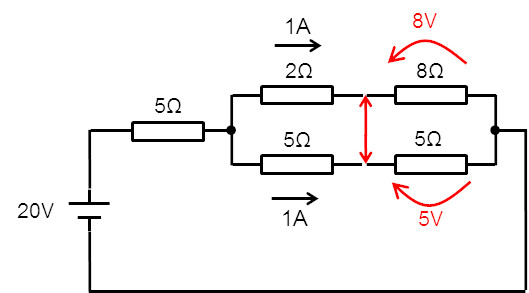
上下両方の抵抗回路ともに電流は 1A だから、各抵抗の両端の電圧を求めると、8Ω抵抗の両端は 8V、5Ω抵抗では 5V になる。

ここまでくれば、この問題で求める a-b間の電圧 V_a-b は、赤色の両矢印で示した部分の電圧(電位差)だから、

V_a-b = 8 – 5 = 3 [V]

と求めることができる。

動画のほうが分かりやすい方はこちらから。

抵抗だけの直流回路はサービス問題。必ず正解しよう。

このタイプの問題を解く手順は次の通り。