問題 <R3年午後問7>
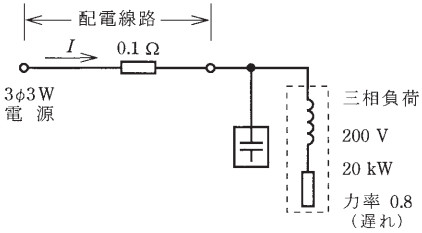
図のように三相電源から、三相負荷 (定格電圧 200V、定格消費電力 20kW、遅れ力率 0.8) に電気を供給している配電線路がある。配電線路の電力損失を最小とするために必要なコンデンサの容量 [kvar] は。
ただし、電源電圧および負荷インピーダンスは一定とし、配電線路の抵抗は 1線当たり 0.1Ω で、配電線路のリアクタンスは無視できるものとする。
<解答の選択肢>
(計算問題のため、選択肢省略)
【出典:令和3年度第一種電気工事士筆記試験-午後問7】
必要なコンデンサ容量は 15[kvar]
解法と解説
方針
交流回路の力率改善はときどき出題される。力率は確実に得点できるように、その後、力率改善の順でマスターしていこう。
ふくラボ流攻略法
配電線路での電力損失を最小にするためには、電流 I を最小にすれば良い。
三相交流回路の皮相電力、有効電力、力率の関係は、
![]()
問題文に与えられている三相負荷の仕様(?)を代入してゴニョゴニョ変形すると、
√3 VI = 20,000/0.8
次、同じ回路における無効電力 Q は、力率の関係式の cosθ を sinθ で置き換えれば良い。そして、cosθ = 0.8 のとき、sinθ = 0.6 と計算できる。したがって、この配電線路の Q は、
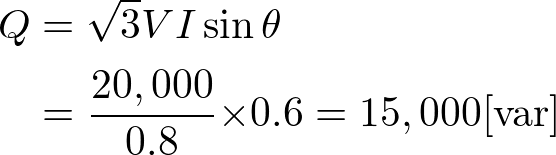
配電線路での電力損失を最小にするには I を最小にすれば良いのだが、それには無効電力 Q を最小、可能ならば 0 [var] にすれば良い。
したがって、電力損失を最小にするために必要なコンデンサ容量は 15kvar。
まとめ
三相交流回路の皮相電力、有効電力、力率の関係は、
![]()
類似問題・関連記事
同じ年度の問題
・前の問題(問6)
・次の問題(問8)
・令和3年度-午後問題
