問題 <R3年午後問6>
図のような、三相3線式配電線路で、受電端電圧が 6,700V、負荷電流が 20A、深夜で軽負荷のため力率が 0.9 (進み力率) のとき、配電線路の送電端の線間電圧 [V] は。
ただし、配電線路の抵抗は 1線当たり 0.8Ω、リアクタンスは 1.0Ω であるとする。
なお、cos θ=0.9 のとき sin θ=0.436 であるとし、適切な近似式を用いるものとする。

<解答の選択肢>
(計算問題のため、選択肢省略)
【出典:令和3年度第一種電気工事士筆記試験-午後問6】
送電端の線間電圧は 6,710V
解法と解説
方針
ふくラボでは公式の丸暗記はほとんどお勧めしないのだが、電路にインダクタンス成分があるときの電路での電圧降下を求める問題だけは公式の丸暗記をお勧めしている…無念…
ふくラボ流攻略法
問題文で示されているような三相交流電路において、電路での電圧降下は次の近似式で計算できる。
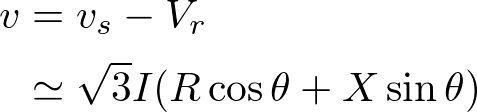
ここで、v : 電路での電圧降下、vs : 送電端電圧、vr : 受電端電圧、I : 配電線路を流れる電流。R : 電路の抵抗成分、X : 電路のインダクタンス(リアクタンス)成分。cosθ : 配電線路に接続されている負荷の力率。
問題文から、
I = 20[A]
R = 0.8[Ω]
X = 1[Ω]
cosθ = 0.9 → sinθ = 0.436
これらの数値を電圧降下の近似式に代入、計算すると v = 10.87…[V]
受電端電圧 vr = 6,700[V] だから、求める送電端電圧は vs = 6,710.8…[V]
まとめ
三相交流電路において、電路での電圧降下は次の近似式で計算できる。
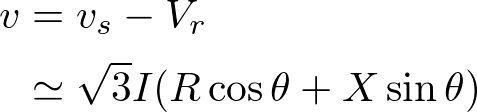
類似問題・関連記事
同じ年度の問題
・前の問題(問5)
・次の問題(問7)
・令和3年度-午後問題
