問題 <2019年問2>
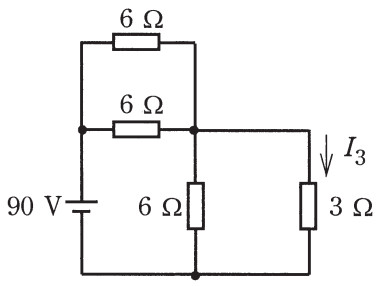
図の直流回路において、抵抗 3Ω に流れる電流 I3 の値 [A] は。
— 答え —
電流 I3 は 12A である。
同じ年度の問題
・前の問題(問1)
・次の問題(問3)
・平成31年度(2019年度)問題
直流回路の電圧・電流を求める問題では、オームの法則を使って既知の値から順に計算していく手順が重要になります。
こうした段階的な計算の流れは、文章よりも動画で見たほうが圧倒的にわかりやすい。
この問題は動画でも丁寧に解説しているので、手順を視覚的に確認したい方は、ぜひ動画版もご活用ください!